Contrôler la propagation des erreurs de calculs numériques
Introduction¶
Lorsque l’on effectue des calculs numériques, ceux-ci sont toujours entachés d’erreurs. C’est le cas notamment lorsque des scientifiques simulent un système physique par des méthodes numériques où une étude mathématique permet de donner une indication sur la précision intrinsèque des méthodes. Par exemple, avec la méthode d’Euler, l’erreur par rapport à la solution réelle du problème diminue avec le pas de temps utilisé. Si l’on faisait les calculs numériques à la main, faire tendre ce pas de temps vers \(0\) nous permettrait de trouver la solution exacte. Évidemment, il est impossible, même pour une machine, d’avoir un pas de temps de \(0\), mais l’on pourrait penser que le réduire autant que notre temps ou puissance de calcul le permet est une bonne chose. Que nenni !
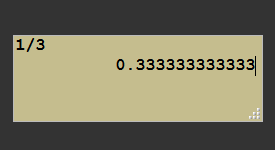
En effet, une deuxième catégorie d’erreurs, qui n’est pas cette fois liée à notre méthode mais bien plus générale, est l’erreur de représentation. Le problème est bien plus trivial, presque grossier dans la simplicité de son énoncé : il est impossible de représenter une quantité infinie dans un espace mémoire de taille finie.
Cela amène à considérer le fait que, quelle que soit la représentation que l’on se donne, c’est-à-dire la manière de traduire un nombre réel pour la machine, alors il existera toujours des nombres pour lesquels la représentation ne sera pas possible. Le jeu des ingénieurs et des chercheurs a été de trouver et formaliser une représentation pratique et la plus intelligente possible, comme compromis entre précision et facilité de manipulation. Ce processus de standardisation a abouti à la norme IEEE-754 suivi par la plupart du matériel informatique mondial.
Attention
Si un rappel général et abstrait sur la représentation des nombres réels en machine est faite par la suite, il est conseillé d’avoir quelques notions sur la représentation des flottants. Des notions de probabilités, notamment sur la construction d’intervalles de confiance, sont recommandées pour aborder la partie théorique.
Une question que l’on se pose naturellement est la suivante : puis-je contrôler numériquement les erreurs qui sont induites par les erreurs de représentation et propagées au cours du calcul ? C’est ce à quoi nous allons tâcher de répondre, par l’affirmative, grâce à la méthode CESTAC, pour Contrôle et Estimation STochastique des Arrondis de Calculs.
Une implémentation de la méthode décrite dans cet article se trouve dans dépôt suivant:
Rappels d’arithmétique flottante¶
Voyons dans un premier temps comment représenter un nombre réel en notation scientifique et dans une base quelconque.
On note \(b\) la base de l’arithmétique dans laquelle nous travaillerons, avec généralement \(b=2\) ou \(b=16\) pour les unités de calculs. Alors, tout nombre \(x\in \mathbb{R}\) peut être écrit de la sorte:
Avec \(\frac{1}{b} \leq m < 1\) et \(m\) la mantisse, possédant possiblement un nombre infini de chiffres après la virgule, et \(e\) un exposant entier lui même exprimé dans la base \(b\).
On peut réécrire la mantisse en base \(b\) par \(\sum_{i}^n m_ib^{-i}, 0 \leq m_i < b\) avec \(n \in \mathbb{N} \cup +\infty\).
Exemple:
On considère \(x = 0,1_{10}\) que l’on voudrait exprimer via cette représentation. Il suffit d’écrire \(x = 0,1 \times 10^0\). Si maintenant on souhaite exprimer \(x\) via cette représentation mais en base \(2\), les choses se compliquent puisque cette fois la mantisse ne possède pas un nombre fini de chiffres ! En effet, par division successive, vous trouverez que \(0,1_{10} = 0,000110011001100..._2\) !
Comme nous l’avons mentionné dans l’introduction, un ordinateur ne disposant que d’une mémoire finie, il est pour lui impossible de stocker une quantité infinie d’information. Or, quelle que soit la base \(b\) choisie, il existe un nombre infini de nombres dont la représensation comporte une mantisse ayant un nombre infini de chiffres1. Autrement dit, il est impossible de représenter parfaitement l’ensemble des réels avec un ordinateur. On approxime généralement ces derniers par des nombres appelés flottants.
C’est ainsi qu’en machine, un nombre réel \(x\) est représenté par un nombre flottant \(X\) qui peut lui même s’écrire de la sorte:
Avec \(\frac{1}{b} \leq M < 1\) et \(M\) la mantisse codée sur un nombre \(n\) fini de digits et \(E\) l’exposant codé également sur un nombre fixe de digits. On peut donc écrire \(M\) en base \(b\) par : \(\sum_{i=1}^n M_ib^{-i}, 0 \leq M_i < b\), où cette fois le nombre d’éléments à sommer est toujours fini.

Comme il ne s’agit que de rappels, je n’entre pas dans toutes subtilités de la norme IEEE-754, et nos explications sont suffisantes pour continuer.
On considère l’opération d’affectation (\(:=\)) : \(\mathbb{R} \to \mathcal{F}\), où \(\mathcal{F}\) est l’ensemble des nombres flottants. C’est-à-dire l’opération qui associe à un réel sa représentation machine.
Pour illustrer concrètement la banalité de la chose via le C++:
1 | |
Pour un réel donné \(x\), il existe un flottant \(X^+\) et un flottant \(X^-\) tels que \(X^- \leq x \leq X^+\) et tel qu’il n’existe pas de flottant \(Y\) et \(Z\) tel que \(X^- < Y < x < Z < X^+\). Autrement dit, \(X^+\) et \(X^-\) sont les flottants immédiatement supérieur et inférieur à \(x\).
Si \(x\) est représentable de manière exacte, alors on a égalité entre les trois termes et l’opération d’affectation \(X := x\) est défini sans ambiguïté.
Si ce n’est pas le cas, comme par l’exemple ci-dessus de \(0,1\) en base 2, il faut choisir entre \(X^+\) et \(X^-\), qui n’ont pas plus de légitimité l’un par rapport à l’autre, à priori.
C’est ici qu’intervient la norme IEEE-754 pour proposer quatre modes d’arrondis permettant de lever l’ambiguïté sur l’opération d’affectation. En voici une description succinte :
- Arrondi vers \(+\infty\) (ou par excès) : on retourne \(X^+\) sauf si \(x = X^-\).
- Arrondi vers \(-\infty\) (ou par défaut) : on retourne \(X^-\) sauf si \(x = X^+\).
- Arrondi vers \(0\) : retourne \(X^-\) pour les positifs et \(X^+\) pour les négatifs.
- Arrondi au plus proche : retourne le nombre machine le plus proche de \(x\).
Une propriété essentielle de la norme IEEE-754 c’est qu’elle garantit que le résultat d’une opération en virgule flottante soit égal au résultat de l’opération réelle correspondante auquel on applique le mode d’arrondi à la suite. Autrement dit, si l’on choisit un arrondi \(Arr\), \(a\) et \(b\) deux réels dont les représentations flottantes sont \(A\) et \(B\), \(+\) une opération réelle, et \(\oplus\) son penchant machine, alors, la norme nous garantit que \(A \oplus B = Arr(a + b)\).
Cette propriété, dite d’arrondi correct, est essentielle car elle permet de faire des preuves sur un algorithme numérique ou d’obtenir des bornes prouvées pour des résultats numériques.
Pour terminer, on peut définir l’erreur relative d’affectation par la formule suivante : \(\alpha = \frac{X - x}{X}\). C’est cette erreur initiale de représentation qui se propage au fur et à mesure des calculs.
Les différents problèmes du numéricien¶
Comme mentionné précédemment, tout algorithme effectuant des calculs en virgule flottante donne un résultat entâché d’erreurs. Lorsqu’un algorithme est fini2, alors l’erreur numérique est le résultat de la propagation des erreurs d’arrondis ou de troncature lors des opérations en virgule flottante.
Dans le cas d’algorithmes itératifs, par exemple la méthode de Newton, présentée par Holosmos dans son cours sur les développements limités, il est en plus nécessaire d’arrêter l’algorithme après un certain nombre, optimal si possible, d’itérations, ce qui est un problème considerant que :
- Si l’algorithme est arrêté trop tôt, la solution obtenue ne sera pas une bonne approximation de la solution cherchée. C’est la vitesse de convergence qui nous informe sur cela, c’est-à-dire les mathématiques derrière une méthode spécifique ;
- Si l’algorithme est arrêté trop tard, des étapes supplémentaires n’apporteront pas plus de précision à la solution obtenue et pire, la propagation des erreurs peut dégrader la solution, jusque, pour les cas pathologiques, obtenir un résultat qui n’a aucun sens.
Ce qu’il faut bien voir ici, c’est qu’étant donnée une méthode numérique itérative, les objectifs du mathématicien et du numéricien sont en quelque sorte opposés : le premier voudrait continuer à itérer autant que faire se peut (c’est-à-dire tant que le matériel le permet) car il sait que cela conduit à une meilleure solution en théorie, tandis que le numéricien nous dit qu’il faut s’arrêter avant (c’est-à-dire bien que le matériel n’est pas contraint physiquement).
En réalité, il y a au moins quatre problèmes intéressants et centraux :
- Pour le mathématicien : comment pour un matériel et un système de représentation des réels donnés puis-je obtenir une meilleure approximation de la solution à mon problème ? Réponse : trouver des algorithmes avec une vitesse de convergence plus grande ou des méthodes pour accélérer la convergence ! On citera à ce propos la méthode du Delta-2 d’Aitken ou l’\(\epsilon\)-algorithme.
- Pour le numéricien : comment pour un algorithme donné ET un matériel et système de représentation des réels donnés, obtenir une meilleure approximation de la solution ? Réponse : réorganiser les opérations de l’algorithme pour limiter la propagation des erreurs de calculs tout en ne changeant pas la vitesse de convergence ! Une technique générique de réorganisation des termes d’une somme pour limiter la propagation des erreurs s’appelle l’algorithme de sommation de Kahan.
- Pour tout le monde : comment pour un algorithme donné et son implémentation, tirer le meilleur de ce dernier ?
Réponses : Choisir une représentation différente des réels, plus adaptée au problème (système de calcul formel,
decimal32, etc. ce qui demande généralement de meilleures performances matérielles) ou augmenter la taille de codage des réels (passage de la simple à la double précision ou quadruple précision, etc. qui ne consiste qu’à augmenter le nombre de bits pour coder la mantisse et l’exposant pour représenter nos réels, ce qui là encore demande de meilleures performances matérielles). - Pour le numéricien : comment déterminer le nombre optimal d’itérations à effectuer pour un algorithme, quelles que soient les données en entrée ? À quelle distance ma solution numérique se trouve-elle de son équivalent réel ? Réponse : Trouver des méthodes d’estimation de la précision numérique d’un résultat, ce qui passe par l’estimation de la propagation des erreurs d’arrondis !
C’est ce dernier problème que s’attache à résoudre la méthode CESTAC que l’on présentera dans la section suivante. Cependant, comme nous le verrons ci-après, on ne peut faire l’économie de quelques connaissances sur les autres problèmes.
Question : N’exagères-tu pas un peu les erreurs de calculs et ne serait-ce pas finalement que des considérations pour chercheurs barbus ? Les erreurs sont-elles si courantes et si importantes ? De ce que j’ai lu, la norme IEEE-754 permet une précision de l’ordre de \(10^{-15}\) en double précision donc mes résultats sont au moins aussi bons non ?
Non, oui, et non. Prenons un cas pathologique extrêmement simple : \(x_n = ax_{n-1} - b\), soit un calcul extrêmement simple. En voici par ailleurs une implémentation en C++, avec une initialisation particulière :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
Ce qui donne pour sortie (consultable directement ici) :
1 2 3 4 5 6 7 8 9 10 11 | |
Autrement dit, alors que le résultat mathématique attendu est \(1\), constant pour chaque itération, après quelques itérations sur machine il y a une divergence très rapide vers l’infini. Après 4 itérations seulement, le nombre de chiffres significatifs entre le résultat réel exact et son penchant flottant est de 0 !
Contrôle et estimation stochastiques des arrondis de calculs¶
Le coeur de CESTAC et la propagation des erreurs¶
L’algèbre \(\mathcal{F}\) sur le corps des nombres flottants n’est pas associative ni distributive. Autrement dit, l’ordre dans lequel on effectue nos opérations arithmétiques a un impact sur le résultat.
La propriété d’arrondi correct permet de garantir la commutativité.
À partir de maintenant, considérons \(f\), une procédure qui travaille sur \(\mathbb{R}\), et son image \(F\), une procédure travaillant sur \(\mathcal{F}\). À cause de la non-associativité, l’image de \(f\) n’est en réalité pas unique et il existe plusieurs procédures qui transcrivent exactement \(f\) du point de vue mathématique. Et évidemment, ces procédures, de par les arrondis de calculs, ne vont pas retourner le même flottant.
Exemple:
Soit la fonction suivante \(f(x) = x^2 + x + 1\). La fonction sur \(\mathcal{F}\) la plus naïve serait \(F_1(X) = (X^2 + X) + 1\) mais l’on pourrait également avoir \(F_2(X) = X^2 + (X + 1)\) ou encore \(F_3(X) = X(X+1) + 1\). Il est évident que sur \(\mathbb{R}\) toutes ces procédures sont exactement les mêmes car elles renvoient exactement le même résultat de par les propriétés d’associativité et de distributivité.
Par contre, ce n’est pas le cas si l’on travaille sur les flottants car tous les résultats intermédiaires seront arrondis. Ainsi, pour un \(X\) fixé, il est tout à fait possible que \(F_1(X) \neq F_2(X) \neq F_3(X)\).
Exemple numérique:
Considérons des nombres flottants avec 6 chiffres de précision. Prenons \(x=1.23456\times 10^{-3}\), \(y=1.00000\times 10^{0}\) et \(z = -y\). Si l’on effectue le calcul \((x + y) + z\), on trouve \(1.23000\times 10^{-3}\), cependant, le calcul \(x + (y + z)\) donnera \(1.23456\times 10^{-3}\). On voit donc que l’ordre des opérations importe.
Comme dans la réalité, les algorithmes sont une succession de petites opérations de calculs, comme celle de l’exemple ci-dessus sur l’évaluation d’un polynôme, le résultat calculé va propager les erreurs opération après opération. Dans les scénarios optimistes, les erreurs se compensent ou sont trop faibles et le résultat est remarquablement proche de ce que permet la précision de la représentation (quoiqu’il en soit, il est impossible de dépasser 16 chiffres significatifs en double précision, par définition !), mais dans le pire des scénarios, le résultat peut être totalement aberrant.
Exemple:
Propagation de l’erreur de l’addition. Considérons \(x\) et \(y\) deux réels et leurs représentations machines \(X\) et \(Y\) entâchées respectivement d’une erreur \(\epsilon_x\) et \(\epsilon_y\).
Que se passe-t-il lorsque nous les ajoutons ?
Celles-ci s’ajoutent entre elles et surtout, s’ajoutent au résultat exact qu’est \(x+y\). Si nous additions à ce résultat un troisième flottant, nous obtiendrons un nouveau terme d’erreur, etc. Le résultat obtenu en machine sera d’autant plus loin du résultat exact que la somme des erreurs ne sera pas négligeable devant les termes exacts (ici \(x\) et \(y\)).
En résumé, à partir d’une procédure \(f\) sur le corps des réels, il existe plusieurs procédures \((F_i)_{0 \leq i < K}\) que l’on obtient en permutant les opérations élémentaires et qui offrent théoriquement, et dans le pire des cas, \(K\) différents résultats. S’ajoute à cela une perturbation du résultat par le mode d’arrondi choisi qui vient encore grossir le pire des cas 3.
Le coeur de CESTAC est de tirer parti de la grande variabilité des résultats obtenus par perturbations des résultats d’une opération et permutations des opérandes afin d’estimer le nombre de chiffres significatifs d’un résultat numérique. En propageant les erreurs de calculs de manières différentes, et aléatoires, on sera capable d’estimer la partie variable parmi les résultats obtenus - la partie entâchée d’erreurs, ou non représentative -, de la partie fixe - la partie exacte -.
À la recherche du nombre de chiffres significatifs¶
Si l’on dispose d’une procédure \(F\) que l’on exécute \(N\) fois avec une perturbation et permutation aléatoires à chaque fois, on obtient un échantillon \(R = (R_0, R_1, ... , R_{N-1})\) de résultats. On peut donc considérer \(F\) comme une variable aléatoire à valeurs dans \(\mathcal{F}\), avec une espérance \(\mu\) et un écart-type \(\sigma\). L’espérance \(\mu\) peut être interprétée comme le résultat attendu de l’algorithme, c’est-à-dire le nombre à virgule flottante qui code notre solution réelle \(r\). L’erreur par rapport à cette espérance, c’est-à-dire \(\alpha = |r - \mu|\) est la perte de précision que l’on est en droit d’attendre du fait d’effectuer des calculs en virgule flottante. Le problème est que \(\mu\) n’est pas connue, et donc, on va l’estimer.
Dans ce cadre, avec pour hypothèse que les éléments de \(R\) sont issus d’une distribution gaussienne (ce qui est vérifié en pratique), le meilleur estimateur de \(\mu\) est la moyenne de l’échantillon \(R\) : \(\(\bar R = \frac 1 N \sum^N_i R_i\)\)
De la même manière, le meilleur estimateur de \(\sigma^2\) est donné par: \(\(S^2 = \frac 1 {N-1} \sum^N_i (R_i - R)^2\)\)
Un usage classique du théoreme central limite nous permet de construire un intervalle de confiance pour la valeur exacte \(r\) pour un seuil \(p\) :
Où \(t_{N-1}(p)\) est la valeur de la fonction de répartition de Student pour \((N-1)\) degrès de libertés et un seuil de \(p\).
À partir de cet intervalle, il est possible de calculer le nombre de chiffres significatifs décimaux \(C\) de notre estimateur \(\bar R\) :
où \(K\) ne dépend que de \(N\) et \(p\), et qui tend vers \(0\) avec \(N\) qui augmente. La valeur de \(p\) est fixée en pratique à \(0.05\), ce qui permet d’obtenir un intervalle de confiance à \(95\%\). Voici maintenant la valeur de \(K\) obtenue en fonction de \(N\), pour \(p = 0.05\) :
| N | K |
|---|---|
| 2 | 1.25 |
| 3 | 0.396 |
Cela peut paraître peu mais comme pour \(N=3\), \(K\) est déjà inférieur à \(1\), en moyenne, il n’y a pas de perte de chiffre significatif à utiliser cette valeur comme taille pour l’échantillon \(R\). En fait, augmenter ce nombre est inutile car la longueur de l’intervalle évoluant en \(\frac 1 N\), pour obtenir un chiffre significatif supplémentaire, il faudrait multiplier \(N\) par 100 (à cause du \(\log_{10}\)) !
La construction de l’échantillon \(R\)¶
Maintenant que nous avons la théorie, il nous faut savoir comment construire un échantillon \(R\) de résultats qui soit le plus représentatif possible de la multitude des résultats obtenables à partir de notre procédure \(F\).
Pour cela, on dispose d’une fonction de perturbation, pert, qui pour un flottant \(X\) particulier, renvoie un flottant perturbé \(X'\) tel que \(X'\) soit \(X\) auquel on a modifié le dernier bit de mantisse de manière aléatoire et uniforme. Il s’agit d’ajouter au dernier bit de mantisse \(-1\), \(0\) ou \(1\) en mode arrondi avec une probabilité de \(\frac 1 3\).
Cette perturbation consiste à choisir aléatoirement parmi \(X^+\) et \(X^-\), que nous évoquions dans la première partie, et ce, afin de simuler la propagation des erreurs d’arrondis.
On utilise pert à chaque fois qu’une affectation est effectuée, qu’il s’agit d’une affectation initiale comme déclaration de variable flottante, ou le résultat de multiples calculs.
On dispose également d’un opérateur de permutation, perm, qui à chaque opérateur d’affectation va modifier aléatoirement le terme de droite en effectuant l’une des permutations autorisées par l’associativité et la distributivité. Autrement dit, il s’agit de choisir entre \(F_1\), \(F_2\) ou \(F_3\) dans l’exemple ci-dessus.
Remarque:
En fait, en théorie, on pourrait aller plus loin en permutant toutes les opérations indépendantes entre elles, c’est-à-dire en réorganisant purement et simplement l’algorithme autant que faire se peut. En pratique on ne le fait pas, notamment car c’est très compliqué pour un gain pas très intéressant.
Attention
Dans la vraie vie, nous sommes au courant des différents pièges posés par la stabilité des calculs numériques et comment les déjouer, notamment en organisant correctement nos calculs (par exemple, sommer des nombres par ordre croissant limite la propagation d’erreurs), ou en utilisant des mécanismes de compensation d’erreurs (citons par exemple l’algorithme de sommation de Kahan). C’est d’ailleurs l’objectif du problème 2. évoqué plus haut. De fait, à partir du moment où l’on optimise sciemment l’ordre des opérations, l’utilisation de perm devient inutile car menant à un intervalle de confiance élargi à tort, et donc une surestimation des erreurs (en plus d’un surcoût non negligeable de calcul).
Ainsi, on ne considerera pas les permutations dans la suite.
À partir de là, il existe deux manières d’utiliser pert pour créer un échantillon \(R\) et estimer le nombre de chiffres significatifs d’un résultat numérique.
Utilisation asynchrone¶
L’utilisation asynchrone consiste à effectuer nos perturbations à chaque affectation, et à construire notre échantillon \(R\) comme le resultat de \(N\) appels à notre procedure \(F\). Autrement dit, les \(N\) appels sont indépendants, d’où le nom asynchrone. Une fois l’échantillon à notre disposition, on calcule le nombre de chiffres significatifs a posteriori.
Illustration de la méthode asynchrone avec une suite itérative définit par \(X_n = F(X_{n-1})\) et pour terme initial \(X_0\) avec \(N=3\):
D’apparence logique, cette méthode se heurte à deux problemes majeurs.
- La propagation des erreurs ne se faisant pas nécessairement de la même manière, il est possible que les exécutions de la procédure converge vers des réels différents, auquel cas l’échantillon est incohérent. Cela peut être le cas si le problème à résoudre admet plusieurs solutions par exemple.
- D’une exécution à l’autre, comme il y a certainement des embranchements conditionnels, deux résultats peuvent provenir d’une suite d’embranchements différents à cause des erreurs d’arrondis. Dès lors il n’est pas pertinent de comparer ces résultats.
Pour ces deux raisons, la version asynchrone est inapplicable en général.
Utilisation synchrone¶
La version synchrone consiste cette fois à faire évoluer l’échantillon à chaque opération d’affectation et utiliser la moyenne empirique de celui-ci pour les embranchements4. Il est possible de donner une estimation du nombre de chiffres significatifs à tout moment car on dispose de l’échantillon à tout moment durant l’exécution. De fait, cela répond aux deux problématiques de la version asynchrone :
- À chaque étape, le résultat est consistant avec lui même, il ne peut s’agir de différentes solutions puisqu’il n’y a jamais qu’une seule valeur qui est utilisée pour les structures conditionnelles.
- La série d’embranchements sera nécessairement unique par construction, ce qui rend le résultat final cohérent.
Illustration de la méthode synchrone sur le même exemple que précédemment :
Remarquez les points de synchronisation après chaque étape, d’où le nom de méthode synchrone, là où dans la méthode asynchrone les \((X^i_j) ~ \forall 0 \leq i < N\) sont indépendants.
CESTAC sur un algorithme itératif¶
Maintenant que nous savons comment déterminer le nombre de chiffres significatifs d’un résultat numérique, on va s’intéresser au problème d’arrêt optimal. La solution exacte à un problème que l’on se propose de résoudre est notée \(x^*\). On dispose d’un algorithme itératif, qui donne à l’itération \(k\), la solution approchée \(x_k\) et l’on sait que cet algorithme converge après un nombre fini ou non d’étapes, c’est-à-dire que \(x_k \to x^*\).
Enfin, on dispose d’une implémentation de notre algorithme qui à chaque itération fournit une solution approchée \(X_k\) entâchée des erreurs numériques.
Un critère classique pour arrêter un algorithme itératif à une précision donnée est le test \(||x_k - x_{k-1}|| < \epsilon\), où \(\epsilon\) fixé, contrôle la précision. Une variante est donnée par \(||x_k - x_{k-1}|| < ||x_k||\epsilon\). Ce test est extrêmement robuste en arithmétique usuelle possédant une précision infinie puisqu’il permet de détecter lorsqu’une itération n’apporte plus de gain significatif à la précision de la solution. À contrario, en arithmétique flottante, comme tous les \(X_k\) sont entâchés d’erreurs, la soustraction de termes très proches conduit à des petites valeurs qui peuvent ne plus être significatives du tout.
Le pire scénario possible est le suivant : \(\epsilon\) est choisi trop petit, et les erreurs de calculs qui se sont accumulées sont trop grandes en comparaison de \(\epsilon\), ce qui fait que l’algorithme ne convergera jamais, sa solution se dégradera pour soit converger vers une valeur incohérente, soit diverger purement et simplement !
Définition (zéro machine):
Une valeur \(X \in \mathcal{F}\), résultat d’un calcul numérique, avec un nombre \(C\) de chiffres significatifs, est un zéro machine si \(X=0\) et \(C > 1\) ou \(X\) est quelconque mais \(C = 0\). On note un zéro machine \(\bar 0\).
Attention
La notion de zéro machine ne doit pas être confondue avec la notion d’epsilon machine ni avec le zéro tel qu’il est représenté dans la norme IEE754.
Comme CESTAC a très exactement pour rôle de déterminer le nombre de chiffres significatifs d’un résultat, on peut donc l’utiliser pour trouver les zéros machines et modifier notre test d’arrêt en conséquence, qui devient le suivant à l’itération \(k\) :
- Si \(C(X_k) = 0\) et \(X_k \neq 0\), alors le résultat est entâché d’une erreur plus grande que sa propre valeur et il ne sert à rien de continuer : on arrête l’algorithme.
- Si \(||X_n - X_{n-1}|| = \bar 0\), on arrête l’algorithme puisque la différence entre deux itérations ne représente que des erreurs de calculs.
- Si le nombre d’itérations dépasse une certaine limite \(K\), la suite est considérée comme non convergente et l’on arrête l’algorithme.
Allez plus loin : discussions sur la validité de CESTAC¶
Information : Cette section est destinée à discuter de manière plus avancée les hypothèses de validité de la méthode CESTAC et peut donc être mise de côté pour une première lecture, d’autant qu’elle peut s’avérer un peu plus technique.
Il y a plusieurs hypothèses qui ont été formulées afin d’aboutir à la formule du nombre de chiffres significatifs et qui amènent à se poser la question suivante : peut-on raisonnablement utiliser un test de Student afin d’obtenir l’intervalle de confiance ? Cela revient à se demander si l’estimateur \(\bar X\) utilisé est biaisé ou non.
Le biais de l’estimateur¶
Sans faire de démonstration et en référant à des résultats d’études des créateurs de la méthode CESTAC, tentons de donner les grandes lignes justifiant le biais nul de l’estimateur de la moyenne empirique.
Théorème:
Un résultat \(X\) d’une procédure \(F\), perturbé, peut s’écrire : $$X = x + \sum _{i = 1}^n d_i 2^{-t}(\alpha_i - h_i) + O(2^{-2t}) $$
Où \(x\) est le résultat exact, \(n\) le nombre d’affectations et d’opérations arithmétiques effectuées par \(F\), \(d_i\) des quantités ne dépendant que des données et de la procédure \(F\), \((\alpha_i)_i\) les erreurs d’arrondis ou de troncature et \((h_i)_i\) les perturbations effectuées.
Le biais de l’estimateur \(\bar X\) est la quantité \(E[\bar X] - x\) . En supposant que les \((\alpha_i)_i\) suivent une distribution uniforme sur l’intervalle « qui va bien »5, il suffit de choisir correctement les \((h_i)_i\) pour recentrer les \((\alpha_i)_i\) et ainsi obtenir le résultat suivant, en négligeant les termes d’ordre supérieur : $$X’ = x + \sum _{i = 1}^n d_i 2^{-t}(z_i) $$
Où les \(z_i\) sont des variables identiquement distribuées et centrées, de sorte que \(E(X') = x\), rendant le biais de notre estimateur nul.
L’hypothèse de la distribution des \(\alpha_i\) est validée dès lors qu’il y a suffisamment d’opérations dans la procédure \(F\), autrement dit que \(n\) est suffisamment grand. En fait, très précisément, le biais n’est pas nul mais l’on peut montrer qu’il est de l’ordre de quelques \(\sigma\) ce qui fausse l’estimation finale de moins d’un chiffre significatif.
La validité du test de Student¶
Comme nous l’avons vu, l’hypothèse de répartition des \(\alpha_i\) est satisfaisante en théorie et en pratique. Mais par contre, pour arriver à ne plus avoir de biais nous avons fait une hypothèse supplémentaire, celle que les termes d’ordre supérieur sont négligeables.
Or, s’il est facile de voir que l’addition ou la soustraction ne créent pas d’erreur d’ordre \(2\), ce n’est pas le cas de la multiplication ou de la division, puisqu’en considérant \(X_1 = x_1 + \epsilon_1\) et \(X_2 = x_2 + \epsilon_2\), ces opérateurs s’écrivent :
Le problème pour la multiplication est que si les erreurs \(\epsilon\) respectives des deux opérandes sont prépondérantes devant les valeurs exactes \(x\), alors le terme d’ordre \(2\) devient prépondérant. Pour la division, les termes d’ordres supérieurs deviennent prépondérants si \(\epsilon_2\) l’est devant \(x_2\).
Dès lors, il existe deux manières complémentaires pour aider à respecter ces contraintes de validité de la méthode CESTAC :
- Augmenter la précision de la représentation, c’est-à-dire coder chaque réel sur plus de bits, ce qui fera diminuer les \(\epsilon\). Autrement dit, la réponse au problème 3.
- Limiter au maximum la propagation des erreurs de calculs, c’est-à-dire appliquer les recettes en réponse au problème 2.
Une approche systématique envisageable consiste à inclure un contrôle dynamique sur le résultat des opérations de multiplication ou division, moyennant un coût important.
Conclusion : CESTAC, mais pour quoi et pour qui ?¶
Nous avons vu les différents problèmes qui apparaissent dès lors que l’on effectue des calculs en virgule flottante et nous avons donné une technique robuste afin de contrôler la propagation des erreurs induites par ces calculs. Après avoir présenté les fondements de la méthode et les modalités d’utilisation, nous avons appliqué CESTAC au problème d’arrêt optimal d’un algorithme itératif. Enfin, une dernière partie fut consacrée à la discussion sur la validité de la méthode et une esquisse de preuve dans l’idée.
La seule question qui n’a pas été abordée, et qui nous servira de conclusion, est : quand utiliser CESTAC ? Il est bien évident que la méthode présente un coût important en temps de calcul, qui doit pouvoir être justifié par un gain au moins aussi important. La nécessité d’évaluation et de contrôle des erreurs est par exemple un point crutial pour les systèmes critiques tels que les avions. C’est d’ailleurs pour cette raison que la méthode est très utilisée dans le domaine de l’aéro-nautique, afin de contrôler à la fois les simulations mais aussi directement les calculs au sein des sytèmes embarqués.
Bibliographie¶
Afin d’écrire cet article, je me suis principalement basé sur les ouvrages, articles ou documents suivants. J’invite donc le lecteur désireux d’en savoir plus à consulter ces ouvrages, malheureusement pour la plupart payants, mais dont des extraits sont disponibles sur Internet légalement et gratuitement.
- Ingénierie du contrôle de la précision des calculs sur ordinateur, Michèle Pichat et Jean Vignes.
- Validité du logiciel numérique, Jean-Marie Chesnaux, support de cours dispensé à l’UPMC.
- Approche stochastique de l’analyse des erreurs d’arrondi : méthode CESTAC, Jean Vignes et René Alt.
- Handbook of Granular Computing, Witold Pedrycz, Andrzej Skowron et Vladik Kreinovich.
-
Donnons une preuve succinte. Par définition, un nombre normal est un nombre tel que toute suite finie de bits apparait un nombre infini de fois dans la mantisse de ce nombre et la probabilité d’apparition des suites est uniforme. Il est dit normal en toute base si quelle que soit la base il est normal. Grâce au lemme de Borel-Cantelli on prouve que l’ensemble des nombres non-normaux en toute base est de mesure nulle. Donc en tirant un nombre au hasard sur \(\mathbb{R}\), quelle que soit la base considérée, la probabilité que le nombre soit normal est 1. \(\square\) ↩
-
où fini s’entend comme un nombre fini d’étapes pour trouver la solution à un probleme, ↩
-
J’insiste sur le fait qu’il s’agit du pire des cas qui est loin d’être une réalité pratique. Or, les études déterministes classiques raisonnent principalement sur le pire des cas ce qui conduit à une surestimation des erreurs de calculs rendant parfois caduque ces méthodes. Au contraire, CESTAC permet de ne pas tomber dans ce piège-là par construction même de la méthode. ↩
-
En pratique, peut aussi utiliser systématiquement \(X_i\) pour un \(i\) donné, ce qui évite de faire le calcul de la moyenne à chaque fois. ↩
-
Cet intervalle dépend de si l’on se place en mode de troncature ou d’arrondi. ↩

 0000-0002-5865-6403
0000-0002-5865-6403